Fundamental Geometry Theorems and Proofs: Episode I.7

Today I prove a simple euclidean geometry theorem.

Let point M be a point outside a circle C that has radius R. Let a be the distance between the point M and the center of the circle C.

Prove that for any line that passes through the point M, and that cuts the circle C in two points A and B, it happens that |MA|*|MB| has a constant value of (a^2 - R^2) for any A,B.

Where |MA| is the distance from M to A and

           |MB| is the distance from M to B.

Proof:

Let T be a point in the border of the circle C such that it is also in one of the two possible tangent lines to circle C that pass through point M. Then the line |MT| is perpendicular to the radius of the circle passing through point T, 

and hence we have |MT|^2 + R^2 = a^2 as shown below thanks to Pythagoras.

Then we can derive that a^2 - R^2 = |MT|^2 from that.

Now all we have to do is prove that |MT|^2 = |MA|*|MB| and we'd be done.

Let's do just that. Take now only into consideration the circle C, the line |MT|, and the line through M,A, and B.

Look now at triangles MAT and  MTB see that they are similar triangles.  

Angles    MTA = MBT because they are both angles with vertex in the border of the circle C and they are both opposed to the same arc.

Angle 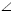MTA is a common angle for both triangles 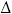MAT and  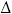MTB.

Hence we have that  ( |MA| / |MT| ) = ( |MT| / |MB| ) which is the same as
|MT|^2 = |MA|*|MB|.



QED.